An assembly language programmer has to know how the hardware implements these cardinal data types. Some examples: Two basic issues are bit ordering (big endian or little endian) and number of bits (or bytes). The assembly language programmer must also pay attention to word length and optimum (or required) addressing boundaries. Composite data types will also include details of hardware implementation, such as how many bits of mantissa, characteristic, and sign, as well as their order. In many cases there are machine specific encodings for some data types, as well as choice of Character codes (such as ASCII or EBCDIC) for character and string implementations.
data size
The basic building block is the bit, which can contain a single piece of binary data (true/false, zero/one, north/south, positive/negative, high/low, etc.).
Bits are organized into larger groupings to store values encoded in binary bits. The most basic grouping is the byte. A byte is the smallest normally addressable quantum of main memory (which can be different than the minimum amount of memory fetched at one time). In modern computers this is almost always an eight bit byte, so much so that many skilled programmers believe that a byte is defined as being always eight bits. In the past there have been computers with seven, eight, twelve, and sixteen bits. There have also been bit slice computers where the common memory addressing approach is by single bit; in these kinds of computers the term byte actually has no meaning, although eight bits on these computers are likely to be called a byte. Throughout the rest of this discussion, assume the standard eight bit byte applies unless specifically stated otherwise.
A nibble is half a byte, or four bits.
A word is the default data size for a processor. The default size does not apply in all cases. The word size is chosen by the processor’s designer(s) and reflects some basic hardware issues (such as internal or external buses). The most common word sizes are 16 and 32, but words have ranged from 16 to 60 bits. Typically there will be additional data sizes that are defined relative to the size of a word: halfword, half the size of a word; longword, usually double the size of a word; doubleword, usually double the size of a word (sometimes double the size of a longword); and quadword, four times the size of a word. Whether or not there is a space between the size designation and “word” is designated by the manufacturer, and varies by processor.
Some processors require that data be aligned. That is, two byte quantities must start on byte addresses that are multiples of two; four byte quantities must start on byte addresses that are multiples of four; etc. The general rule follows a progression of exponents of two (2, 4, 8, 16, ƒ). Some processors allow data to be unaligned, but this usually results in a slow down in performance.
- DEC VAX 16 bit [2 byte] word; 32 bit [4 byte] longword; 64 bit [8 byte]quadword; 132 bit [16 byte] octaword; data may be unaligned at a speed penalty
- IBM 360/370 32 bit [4 byte] word or full word (which is the smallest amount of data that can be fetched, with words being addresses by the highest order byte); 16 bit [2 byte] half-word; 64 bit [8 byte] double word; all data must be aligned on full word boundaries
- Intel 80x86 16 bit [2 byte] word; 32 bit [4 byte] doubleword; data may be unaligned at a speed penalty
- MIX byte of unspecified size, must work for both binary and decimal operations without programmer knowledge of size of byte, must be able to contain the values 0 to 63, inclusive, and must not hold more than 100 distinct values, six bits on a binary implementation, two digits on a decimal implementation; word is one sign and five bytes
- Motorola 680x0 8 bit byte; 16 bit [2 byte] word; 32 bit [4 byte] long or long word; 64 bit [8 byte] quad word; data may be unaligned at a speed penalty, instructions must be on word boundaries
- Motorola 68300 8 bit byte; 16 bit [2 byte] word; 32 bit [4 byte] long or long word; 64 bit [8 byte] quad word; data may be unaligned at a speed penalty, instructions must be on word boundaries
endian
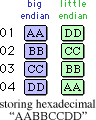
Endian is the ordering of bytes in multibyte scalar data. The term comes from Jonathan Swift’s Gulliver’s Travels. For a given multibyte scalar value, big- and little-endian formats are byte-reversed mappings of each other. While processors handle endian issues invisibly when making multibyte memory accesses, knowledge of endian is vital when directly manipulating individual bytes of multibyte scalar data and when moving data across hardware platforms.
Big endian stores scalars in their “natural order”, with most significant byte in the lowest numeric byte address. Examples of big endian processors are the IBM System 360 and 370, Motorola 680x0, Motorola 68300, and most RISC processors.
Little endian stores scalars with the least significant byte in the lowest numeric byte address. Examples of little endian processors are the Digital VAX and Intel x86 (including Pentium).
Bi-endian processors can run in either big endian or little endian mode under software control. An example is the Motorola/IBM PowerPC, which has two separate bits in the Machine State Register (MSR) for controlling endian: the ILE bit controls endian during interrupts and the LE bit controls endian for all other processes. Big endian is the default for the PowerPC.
number systems
Binary is a number system using only ones and zeros (or two states).
Decimal is a number system based on ten digits (including zero).
Hexadecimal is a number system based on sixteen digits (including zero).
Octal is a number system based on eight digits (including zero).
Duodecimal is a number system based on twelve digits (including zero).
| binary | octal | decimal | duodecimal | hexadecimal |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 | 8 |
| 1001 | 11 | 9 | 9 | 9 |
| 1010 | 12 | 10 | A | A |
| 1011 | 13 | 11 | B | B |
| 1100 | 14 | 12 | 10 | C |
| 1101 | 15 | 13 | 11 | D |
| 1110 | 16 | 14 | 12 | E |
| 1111 | 17 | 15 | 13 | F |
| 10000 | 20 | 16 | 14 | 10 |
| 10001 | 21 | 17 | 15 | 11 |
| 10010 | 22 | 18 | 16 | 12 |
| 10011 | 23 | 19 | 17 | 13 |
| 10100 | 24 | 20 | 18 | 14 |
| 10101 | 25 | 21 | 19 | 15 |
| 10110 | 26 | 22 | 1A | 16 |
| 10111 | 27 | 23 | 1B | 17 |
| 11000 | 30 | 24 | 20 | 18 |
number representations
integer representations
Sign-magnitude is the simplest method for representing signed binary numbers. One bit (by universal convention, the highest order or leftmost bit) is the sign bit, indicating positive or negative, and the remaining bits are the absolute value of the binary integer. Sign-magnitude is simple for representing binary numbers, but has the drawbacks of two different zeros and much more complicates (and therefore, slower) hardware for performing addition, subtraction, and any binary integer operations other than complement (which only requires a sign bit change).
In one’s complement representation, positive numbers are represented in the “normal” manner (same as unsigned integers with a zero sign bit), while negative numbers are represented by complementing all of the bits of the absolute value of the number. Numbers are negated by complementing all bits. Addition of two integers is peformed by treating the numbers as unsigned integers (ignoring sign bit), with a carry out of the leftmost bit position being added to the least significant bit (technically, the carry bit is always added to the least significant bit, but when it is zero, the add has no effect). The ripple effect of adding the carry bit can almost double the time to do an addition. And there are still two zeros, a positive zero (all zero bits) and a negative zero (all one bits).
In two’s complement representation, positive numbers are represented in the “normal” manner (same as unsigned integers with a zero sign bit), while negative numbers are represented by complementing all of the bits of the absolute value of the number and adding one. Negation of a negative number in two’s complement representation is accomplished by complementing all of the bits and adding one. Addition is performed by adding the two numbers as unsigned integers and ignoring the carry. Two’s complement has the further advantage that there is only one zero (all zero bits). Two’s complement representation does result in one more negative number (all one bits) than positive numbers.
Two’s complement is used in just about every binary computer ever made. Most processors have one more negative number than positive numbers. Some processors use the “extra” neagtive number (all one bits) as a special indicator, depicting invalid results, not a number (NaN), or other special codes.
In unsigned representation, only positive numbers are represented. Instead of the high order bit being interpretted as the sign of the integer, the high order bit is part of the number. An unsigned number has one power of two greater range than a signed number (any representation) of the same number of bits.
| bit pattern | sign-mag. | one’s comp. | two’s comp | unsigned |
| 000 | 0 | 0 | 0 | 0 |
| 001 | 1 | 1 | 1 | 1 |
| 010 | 2 | 2 | 2 | 2 |
| 011 | 3 | 3 | 3 | 3 |
| 100 | -0 | -3 | -4 | 4 |
| 101 | -1 | -2 | -3 | 5 |
| 110 | -2 | -1 | -2 | 6 |
| 111 | -3 | -0 | -1 | 7 |
floating point representations
Floating point numbers are the computer equivalent of “scientific notation” or “engineering notation”. A floating point number consists of a fraction (binary or decimal) and an exponent (bianry or decimal). Both the fraction and the exponent each have a sign (positive or negative).
In the past, processors tended to have proprietary floating point formats, although with the development of an IEEE standard, most modern processors use the same format. Floating point numbers are almost always binary representations, although a few early processors had (binary coded) decimal representations. Many processors (especially early mainframes and early microprocessors) did not have any hardware support for floating point numbers. Even when commonly available, it was often in an optional processing unit (such as in the IBM 360/370 series) or coprocessor (such as in the Motorola 680x0 and pre-Pentium Intel 80x86 series).
Hardware floating point support usually consists of two sizes, called single precision (for the smaller) and double precision (for the larger). Usually the double precision format had twice as many bits as the single precision format (hence, the names single and double). Double precision floating point format offers greater range and precision, while single precision floating point format offers better space compaction and faster processing.
F_floating format (single precision floating), DEC VAX, 32 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 15 bits of an excess 128 binary exponent, followed by a normalized 24-bit fraction with the redundant most significant fraction bit not represented. Zero is represented by all bits being zero (allowing the use of a longword CLR to set a F_floating number to zero). Exponent values of 1 through 255 indicate true binary exponents of -127 through 127. An exponent value of zero together with a sign of zero indicate a zero value. An exponent value of zero together with a sign bit of one is taken as reserved (which produces a reserved operand fault if used as an operand for a floating point instruction). The magnitude is an approximate range of .29*10-38 through 1.7*1038. The precision of an F_floating datum is approximately one part in 223, or approximately seven (7) decimal digits).
32 bit floating format (single precision floating), AT&T DSP32C, 32 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 23 bits of a normalized two’s complement fractional part of the mantissa, followed by an eight bit exponent. The magnitude of the mantissa is always normalized to lie between 1 and 2. The floating point value with exponent equal to zero is reserved to represent the number zero (the sign and mantissa bits must also be zero; a zero exponent with a nonzero sign and/or mantissa is called a “dirty zero” and is never generated by hardware; if a dirty zero is an operand, it is treated as a zero). The range of nonzero positive floating point numbers is N = [1 * 2-127, [2-2-23] * 2127] inclusive. The range of nonzero negative floating point numbers is N = [-[1 + 2-23] * 2-127, -2 * 2127] inclusive.
40 bit floating format (extended single precision floating), AT&T DSP32C, 40 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 31 bits of a normalized two’s complement fractional part of the mantissa, followed by an eight bit exponent. This is an internal format used by the floating point adder, accumulators, and certain DAU units. This format includes an additional eight guard bits to increase accuracy of intermediate results.
D_floating format (double precision floating), DEC VAX, 64 bits, the first bit (high order bit in a register, first bit in memory) is the sign magnitude bit (one=negative, zero=positive or zero), followed by 15 bits of an excess 128 binary exponent, followed by a normalized 48-bit fraction with the redundant most significant fraction bit not represented. Zero is represented by all bits being zero (allowing the use of a quadword CLR to set a D_floating number to zero). Exponent values of 1 through 255 indicate true binary exponents of -127 through 127. An exponent value of zero together with a sign of zero indicate a zero value. An exponent value of zero together with a sign bit of one is taken as reserved (which produces a reserved operand fault if used as an operand for a floating point instruction). The magnitude is an approximate range of .29*10-38 through 1.7*1038. The precision of an D_floating datum is approximately one part in 255, or approximately 16 decimal digits).

0 responce(s):
Post a Comment